CSP-S 2021 初赛 做题笔记
在 Linux 系统终端中,用于列出当前目录下所含的文件和子目录的命令为( )。
A.$\text{ls}$ B.$\text{cd}$ C.$\text{cp}$ D.$\text{all}$
显然答案为 $A$。
二进制数 $00101010_{2}$ 和 $00010110_{2}$ 的和为( )。
A.$00111100_{2}$ B.$01000000_{2}$ C.$00111100_{2}$ D.$01000010_{2}$
显然答案为 $B$。
在程序运行过程中,如果递归调用的层数过多,可能会由于( )引发错误。
A.系统分配的栈空间溢出
B.系统分配的队列空间溢出
C.系统分配的链表空间溢出
D.系统分配的堆空间溢出
递归调用的是栈空间,所以选 $A$。
以下排序方法中,( )是不稳定的。
A.插入排序 B.冒泡排序 C.堆排序 D.归并排序
除了堆排序,其他都是稳定的,所以选 $C$。
以比较为基本运算,对于 $2n$ 个数,同时找到最大值和最小值,最坏情况下需要的最小的比较次数为( )。
A.$4n-2$ B.$3n+1$ C.$3n-2$ D.$2n+1$
首先可以比较 $n$ 次,分出 $a_{i\times 2-1}$ 与 $a_{i*2}$ 中较小的与较大的。显然最小数必然在较小的那组,最大数必然在较大的那组,由于第一个数不用比较,所以最少的比较次数为 $3n-2$,选 $C$。
现有一个地址区间为 $0\sim 10$ 的哈希表,对于出现冲突情况,会往后找第一个空的地址存储 (到 $10$ 冲突了就从 $0$ 开始往后),现在要依次存储 $(0,1,2,3,4,5,6,7)$,哈希函数为 $h(x)=x^{2} \bmod {11}$。请问 $7$ 存储在哈希表哪个地址中( )。
A.$5$ B.$6$ C.$7$ D.$8$
$h(0)=0$;
$h(1)=1$;
$h(2)=4$;
$h(3)=9$;
$h(4)=5$;
$h(5)=4$,因为 $4$,$5$ 都有了,所以 $h(5)=6$;
$h(6)=3$;
$h(7)=5$,因为 $5$,$6$ 都有了,所以 $h(7)=7$。
所以选 $C$。
$G$ 是一个非连通简单无向图(没有自环和重边),共有 $36$ 条边,则该图至少有( )个点。
A.$8$ B.$9$ C.$10$ D.$11$
首先 $9$ 个点最多可以有 $\dfrac{9\times 8}{2}=36$ 条边,但因为 $G$ 是非联通图,于是再加一个点独立成为一个连通块,所以答案为 $C$。
令根结点的高度为 $1$,则一棵含有 $2021$ 个结点的二叉树的高度至少为( )。
A.$10$ B.$11$ C.$12$ D.$2021$
显然高度为 $n$ 的最多有 $2^{n}-1$ 的节点,带入算即可,选 $B$。
前序遍历和中序遍历相同的二叉树为且仅为( )。
A.只有 $1$ 个点的二叉树
B.根结点没有左子树的二叉树
C.非叶子结点只有左子树的二叉树
D.非叶子结点只有右子树的二叉树
前序遍历是先访问根节点,再访问左节点,最后访问右节点;
中序遍历是先访问左节点,再访问根节点,最后访问右节点;
不难发现如果都没有左节点,前序遍历和中序遍历就是一样的。
答案选 $D$。
定义一种字符串操作为交换相邻两个字符。将 $\texttt{DACFEB}$ 变为 $\texttt{ABCDEF}$ 最少需要 ( ) 次上述操作。
A.$7$ B.$8$ C.$9$ D.$6$
操作如下:
$0:\texttt{DACFEB}$;
$1:\texttt{ADCFEB}$;
$2:\texttt{ADCFBE}$;
$3:\texttt{ADCBFE}$;
$4:\texttt{ADBCFE}$;
$5:\texttt{ABDCFE}$;
$6:\texttt{ABCDFE}$;
$7:\texttt{ABCDEF}$;
选 $A$。
有如下递归代码
1
2
3solve(t,n):
if t=1 return 1
else return 5*solve(t-1,n) mod n则
solve(23,23)的结果为( )。A.$1$ B.$7$ C.$12$ D.$22$
不难发现答案为 $5^{22}\bmod 23$,即为 $1$,选 $A$。
斐波那契数列的定义为: $F_{1}=1$,$F_{2}=1$,$F_{n}=F_{n-1}+F_{n-2}$ $(n\geq 3)$。现在用如下程序来计算斐波那契数列的第 $n$ 项,其时间复杂度为( )。
1
2
3F(n):
if n<=2 return 1
else return F(n-1) + F(n-2)A.$O(n)$
B.$O(n^{2})$
C.$O(2^{n})$
D.$O(n\log n)$
模拟一下 $n=5$ 的情况:

可以发现这与满二叉树非常相似,于是选 $C$。
有 $8$ 个苹果从左到右排成一排,你要从中挑选至少一个苹果,并且不能同时挑选相邻的两个苹果,一共有( )种方案。
A.$36$ B.$48$ C.$54$ D.$64$
选一个苹果:$8$ 种;
选两个苹果:$6+5+4+3+2+1=21$ 种;
选三个苹果:$(4+3+2+1)+(3+2+1)+(2+1)+1=20$种;
选四个苹果:$(2+1)+1+1=5$ 种;
所以总共有 $8+21+20+5=54$ 种,选 $C$。
设一个三位数 $n=\overline{abc}$,$a,b,c$ 均为 $1\sim 9$ 之间的整数,若以 $a$、 $b$、 $c$ 作为三角形的三条边可以构成等腰三角形(包括等边),则这样的 $n$ 有( )个。
A.$81$ B.$120$ C.$165$ D.$216$
$a=b=c$:$9$ 种;
$a=b=1$,$a\not= c$:$0<c<2$,$0$ 种;
$a=b=2$,$a\not= c$:$0<c<4$,$2$ 种;
$a=b=3$,$a\not= c$:$0<c<6$,$4$ 种;
$a=b=4$,$a\not= c$:$0<c<8$,$6$ 种;
$a=b=5$,$a\not= c$:$0<c<10$,$8$ 种;
$a=b=6$,$a\not= c$:$0<c<10$,$8$ 种;
$a=b=7$,$a\not= c$:$0<c<10$,$8$ 种;
$a=b=8$,$a\not= c$:$0<c<10$,$8$ 种;
$a=b=9$,$a\not= c$:$0<c<10$,$8$ 种;
接下来还有 $b=c$,$a=c$,与 $a=b$ 种数相同。
于是答案为 $9+(0+2+4+6+8+8+8+8+8)\times 3=165$ 种,选 $C$。
有如下的有向图,节点为 $A,B,\cdots ,J$, 其中每条边的长度都标在图中。则节点 $A$ 到节点 $J$ 的最短路径长度为( )。
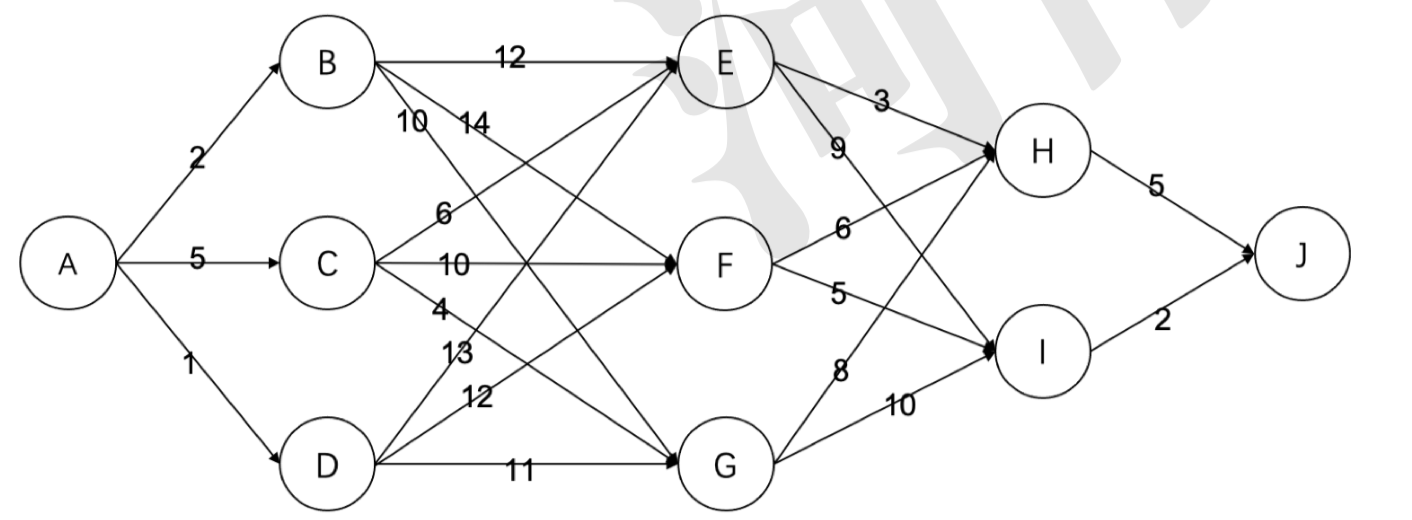
A.$16$ B.$19$ C.$20$ D.$22$
如图中红色路径:

答案为 $B$。

将第 $21$ 行中 $t$ 的类型声明从
int改为double, 不会 影响程序运行的结果。()正确,因为 $sq$ 函数返回值也是
int不会有影响。将第 $26$、$27$ 行中的
/ sqrt(t) / 2替换为/ 2 / sqrt(t),不会影响程序运行的结果。( )错误,因为先除以 $\text{sqrt}$ 会将类型强制转为
double,而先除以 $2$ 不会。将第 $28$ 行中的
x * x改成sq(x)、y * y改成sq(y),不会影响程序运行的结果。( )错误,
x*x返回的是double,而sq(x)返回的是int。当输入为
0 0 0 1 1 0 0 1时,输出为1.3090( )正确,手动模拟一下即可。其中 $r$ 为 $\dfrac{\pi}{3}$。
当输入为
1 1 1 1 1 1 1 2时,输出为( )。A.
3.1416B.
6.2832C.
4.7124D.
4.1888也是手动模拟一下即可,选 $D$。
这段代码的含义为( )。
A.求圆的面积并
B.求球的体积并
C.求球的体积交
D.求椭球的体积并
注意到 $r=\dfrac{\pi}{3}$,而球的体积公式为 $V=\dfrac{4}{3}\pi R^{3}$;第 $23$ 输出的是 $\min(d_{1},d_{2})$,于是可以想到是求球的体积交,选 $C$。


程序总是会正常执行并输出两行两个相等的数。( )
正确,
solve1和solve2都是在求最大子段和。第 $28$ 行与第 $38$ 行分别有可能执行两次及以上。( )
错误,二分到边界时,只会出现 $h=m$ 的情况,如果输入的 $n<0$,则回执行一次。
当输入为
5 -10 11 -9 5 -7时,输出的第二行为7。( )错误,最大子段和为
11,注意第一个数是 $n$。solve1(1, n)的时间复杂度为( )。A.$O(\log n)$
B.$O(n)$
C.$O(n \log n)$
D.$O(n^{2})$
$T(n)=2\times T(\dfrac{n}{2})+1$,$T(n)=2\times n-1$,选 $B$。
solve2(1, n)的时间复杂度为( )。A.$O(\log n)$
B.$O(n)$
C.$O(n \log n)$
D.$O(n^{2})$
$T(n)=2\times T(\dfrac{n}{2})+n$,复杂度是 $O(n\log n)$,选 $C$。
当输入为
10 -3 2 10 0 -8 9 -4 -5 9 4时,输出的第一行为( )。A.$13$
B.$17$
C.$24$
D.$12$
最大子段为
2 10 0 -8 9 -4 -5 9 4,同样需要注意第一个 $10$ 是 $n$,选 $B$。


程序总是先输出 一行 一个整数,再输出 一行 一个字符串。( )
错误,解密的字符串中可能有换行符。
对于任意不含空白字符的字符串
str1,先执行程序输入0 str1,得到输出的第二行记为str2再执行程序输入1 str2,输出的第二行必为str1。( )正确,就是解密与加密。
当输入为
1 SGVsbG93b3JsZA==时,输出的第二行为HelloWorld。( )错误,手动模拟一下发现答案是
Helloworld。设输入字符串长度为 $n$,
encode函数的时间复杂度为( )。A.$O(\sqrt{n})$
B.$O(n)$
C.$O(n\log n)$
D.$O(n^2)$
显然是 $O(n)$,选 $B$。
输出的第一行为( )。
A.
0xffB.
255C.
0xFFD.
-1是 $-1$,可能是操作系统的问题,选 $D$。
当输入为
0 CSP2021csp时,输出的第二行为( )。A.
Q1NQMjAyMWNzcAv=B.
Q1NQMjAyMGNzcA==C.
Q1NQMjAyMGNzcAv=D.
Q1NQMjAyMWNzcA==还是要手动模拟,选 $D$。
(魔法数字) 小 H 的魔法数字是 $4$。给定 $n$, 他希望用若干个 $4$ 进行若干次加法、减法和整除运算得到 $n$。但由于小 H 计算能力有限,计算过程中只能出现不超过 $M=10000$ 的正整数。求至少可能用到多少个 $4$。
例如,当 $n=2$ 时,有 $2=\dfrac{4 + 4}{4}$,用到了 $3$ 个 $4$,是最优方案。

①处应填( )
A.
F[4] = 0B.
F[1] = 4C.
F[1] = 2D.
F[4] = 1得到 $4$ 只需要 $1$ 次,于是
F[4]=1,选 $D$。②处应填( )
A.
!Vis[n]B.
r < nC.
F[M] == INT_MAXD.
F[n] == INT_MAX如果它已经能作为一个最小值可以去更新其他的数,即
Vis[n]==1时答案最优,选 $A$。③处应填( )
A.
F[i] == rB.
!Vis[i] && F[i] == rC.
F[i] < F[x]D.
!Vis[i] && F[i] < F[x]首先得保证当前的 $i$ 不是最优,即
Vis[i]=0,然后找出F[i]中的最小值,选$D$。④处应填( )
A.
F[i] < F[x]B.
F[i]<=rC.
Vis[i]D.
i <= x保证当前的 $i$ 最优即可,用 $x$ 与 $i$ 去更新下一个数,选 $C$。
( RMQ 区间最值问题)给定序列 $a_0,\cdots,a_{n-1}$,$m$ 次询问,每次询问给定 $l,r$,求 $\max \{a_l,\ …,a_r\}$。
为了解决该问题,有一个算法叫 the Method of Four Russians,其时间复杂度为 $O(n+m)$ ,步骤如下:
建立 Cartesian(笛卡尔)树,将问题转化为树上的 LCA(最近公共祖先)问题。
对于 LCA 问题,可以考虑其 Euler 序(即按照 DFS 过程,经过所有点,环游回根的序列),即求 Euler 序列上两点间一个新的 RMQ 问题。
注意新的问题为 $\pm 1$ RMQ,即相邻两点的深度差一定为 $1$。
下面解决这个 $\pm 1$ RMQ 问题,“序列”指 Euler 序列:
设 $t$ 为 Euler 序列长度。取 $b=\lceil \frac{\log_2 t}{2} \rceil$ 将序列每 $b$ 个分为一大块,使用 ST 表(倍增表)处理大块间的 RMQ 问题,复杂度 $O(\frac{t}{b}\log t)=O(n)$
(重点) 对于一个块内的 RMQ 问题,也需要 $O(1)$ 的算法。由于差分数组 $2^{b-1}$ 种,可以预处理出所有情况下的最值位置,预处理复杂度 $O(b2^b)$,不超过 $O(n)$。
最终,对于一个查询,可以转化为中间整的大块的 RMQ 问题,以及两端块内的 RMQ 问题。
试补全程序。
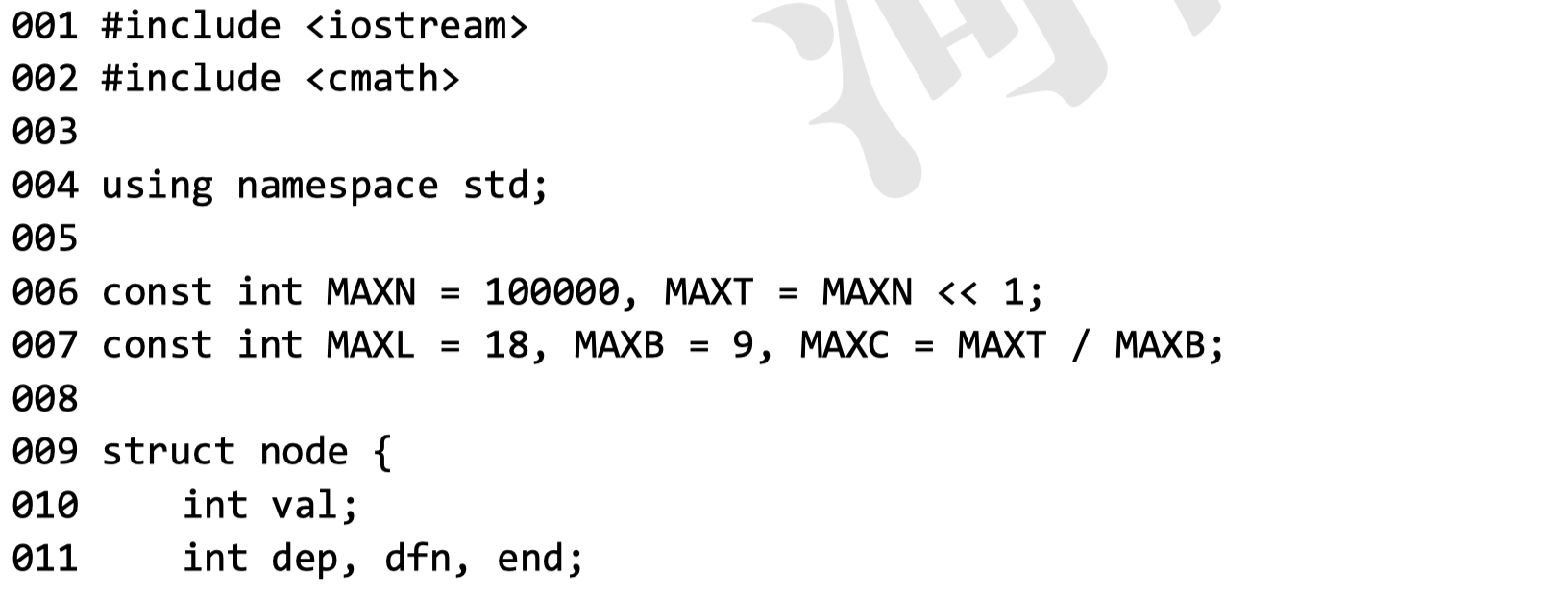



①处应填( )
A.
p->son[0] = S[top--]B.
p->son[1] = S[top--]C.
S[top--]->son[0] = pD.
S[top--]->son[1] = p②处应填( )
A.
p->son[0] = S[top]B.
p->son[1] = S[top]C.
S[top]->son[0] = pD.
S[top]->son[1] = p③处应填( )
A.
x->dep < y->depB.
x < yC.
x->dep > y->depD.
x->val < y->val④处应填( )
A.
A[i * b + j - 1] == A[i * b + j]->son[0]B.
A[i * b + j]->val < A[i * b + j - 1]->valC.
A[i * b + j] == A[i * b + j - 1]->son[1]D.
A[i * b + j]->dep < A[i * b + j - 1]->dep⑤处应填( )
A.
v += (S >> i & 1) ? -1 : 1B.
v += (S >> i & 1) ? 1 : -1C.
v += (S >> (i - 1) & 1) ? 1 : -1D.
v += (S >> (i - 1) & 1) ? -1 : 1⑥处应填( )
A.
(Dif[p] >> (r - p * b)) & ((1 << (r - l)) - 1)B.
Dif[p]C.
(Dif[p] >> (l - p * b)) & ((1 << (r - l)) - 1)D.
(Dif[p] >> ((p + 1) * b - r)) & ((1 << (r - l + 1)) - 1)
神仙题,不会,答案是 $ADADDC$。



