模拟试题：https://wzyqwq.lanzoui.com/iWxKqtujqmb

答案：https://wzyqwq.lanzoui.com/iftwHu726yj?w

1.基础知识

• 计算机的发展

世界上第一台电子计算机：$\color{red}\text{ENIAC}$，于 $\text{1946}$ 年由美固宾夕法尼亚大学的物理学家 约翰·莫克利（$\texttt{John Mauchly}$）和工程师 普雷斯伯·埃克特（$\texttt{J.hesper.Eckert}$）领导研制。

世界上第一台具有存储程序功能的计算机：$\color{red}\text{EDVAC}$，由 冯·诺依曼 设计。

同 ENIAC 相比，EDVAC 方案有两个重大改进：

1. 采用了 $\color{blue}\text{二进制}$。
2. 提出了 $\color{blue}\text{“存储程序”}$ 。

• 与计算机有关的人物：

1. 冯·诺依曼（美）：现代计算机之父，首次提出了存储程序控制原理，称为“冯·诺依曼结构”。
2. 艾伦·麦席森·图灵（英）：计算机科学/人工智能之父，首次提出了计算机科学理论。计算机界的最高奖项 $\color{red}\text{“图灵奖”}$ 以他命名，被称为“计算机界的诺贝尔奖”。
3. 阿达·洛芙莱斯（$\texttt{Ada Lovelace}$）：英国著名诗人 拜伦 的女儿，由于她在程序设计上的开创性工作，被称为世界上 $\color{blue}\text{“第一位程序员”}$，$\color{blue}\text{“世界上第一位软件工程师”}$。
4. 董铁宝：中国第一个程序员，王选 的老师。
5. 姚期智：因对计算理论做出了诸多根本性的重大贡献而获得图灵奖。

• 计算机发展的几个阶段

1. 第一代（$\text{1946}\sim\text{1958}$）：电子管。
2. 第二代（$\text{1958}\sim\text{1964}$）：晶体管。
3. 第三代（$\text{1964}\sim\text{1975}$）：中小规模集成电路。
4. 第四代（$\text{1975}\sim\texttt{至今}$）：大规模／超大规模集成电路。

• 计算机的应用

1. 科学计算（数值计算）。
2. 数据处理（信息处理）。
3. 人工智能。
4. 自动控制。
5. 计算机辅助设计和制造：

• 计算机的组成

1. 硬件系统

五个基本部分组成：运算器，控制器，存储器，输入设备，输出设备。

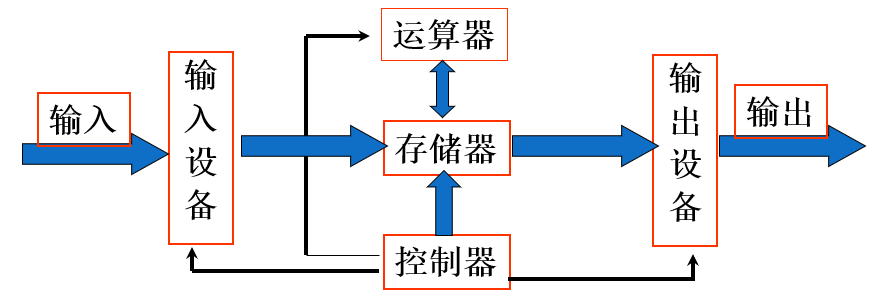
运算器+控制器=CPU（中央处理器），CPU 直接决定计算机的运行速度。

$\text{Eg}$：$\texttt{Intel奔腾IV2.8GHz/512M/80GB/50X}$，每秒运算次数为 $2.8\times 2^{10}\times 2^{10}\times 2^{10}$。

存储器分类：

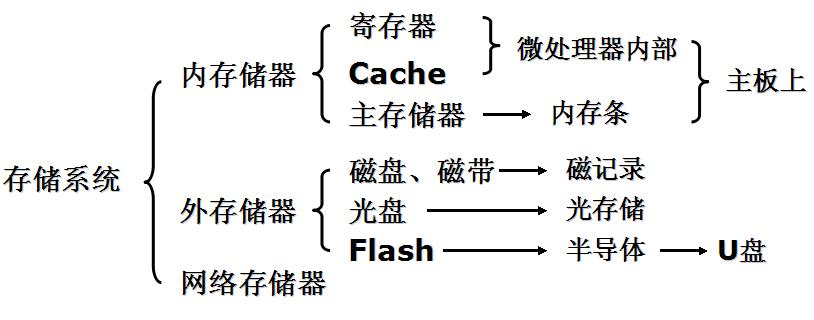
运行速度比较：

寄存器 > $\text{Cache}$ > 内存速度 > 外存速度。

1. 软件系统

分为 系统软件 与 应用软件。

系统软件分为 操作系统软件 与 计算机语言。

操作系统软件：$\color{red}\text{DOS}$，$\color{red}\text{OS/2}$，$\text{windows95}$，$\text{windows98}$，$\text{windows 2000}$，$\text{xp}$，$\text{Vista}$，$\color{red}\text{win7}$，$\text{win8}$，$\color{red}\text{MAC OS}$，$\color{red}\text{Ubuntu}$，$\color{red}\text{win10}$ 等。

计算机语言可分为 机器语言，汇编语言，高级语言 三大类。

机器语言：一台计算机全部的指令集合。

汇编语言：用一些简洁的英文字母、符号串来替代一个特定的指令的二进制串，亦称为 符号语言。

高级语言：$\text{BASIC}$，$\text{C}$，$\text{C++}$，$\text{PASCAL}$，$\text{FORTRAN}$。

应用软件：$\text{Office}$，$\text{3Dmax}$，$\text{Flash}$，$\text{Photoshop}$ 等。

$\text{Ps}$：只有硬件没有安装软件的计算机称为 $\color{blue}\text{“裸机”}$。

面向对象语言：是一类以对象作为基本程序结构单位的程序设计语言，可分为 纯面向对象语言，混合型面向对象语言。

纯面向对象语言有 $\text{Smalltalk}$，$\text{EIFFEL}$ 等。

混合型面向对象语言有 $\text{C++}$，$\text{Objective-C}$ 等。

• 计算机指令系统

指令：计算机能直接识别和执行的命令。

指令本身是二进制代码。是要计算机执行某种操作的命令。

用机器指令编写的程序称之为机器语言程序。

一条指令通常由 $\color{red}\text{操作码}$ 和 $\color{red}\text{地址码}$ 两部分组成。

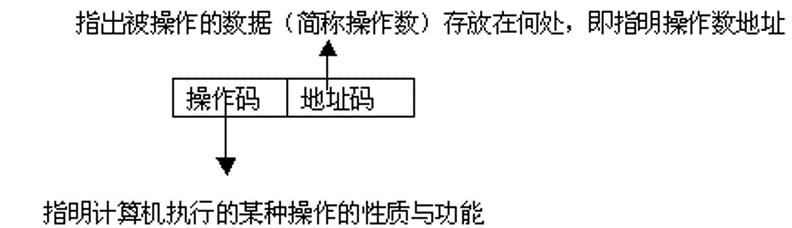
• 计算机的数字系统

数值信息在计算机内的表示方法就是用二进制数来表示。

通常有 $\text{10}$ 进制，$\text{2}$ 进制，$\text{8}$ 进制与 $\text{16}$ 进制。

1. $\text{10}$ 进制转 $\text{R}$ 进制——短除法。

如果有小数，则不断乘 $\text{R}$ 且去整数部分正向输出。

$(0.3125)_{10}$

$0.3125\times 2=0.625\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0$

$0.625\times 2=1.25\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,1$

$0.25\times 2=0.5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0$

$0.5\times 2=1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,1$

所以 $(0.3125)_{10}=(0.0101)_{2}$。

1. $\text{R}$ 进制转 $\text{10}$ 进制——按权展开法。

$(1000101.101)_{2}$

$1\times 2^{-3}+1\times 2^{-1}+1\times 2^{0}+1\times 2^{2}+1\times 2^{6}=69.625$

所以 $(1000101.101)_{2}=(69.625)_{10}$。

1. 特殊：$\text{8}$ 进制转 $\text{16}$ 进制——以二进制为桥梁。

$\text{8}$ 进制表示数：

将 $\text{8}$ 进制数每位数用 $\text{2}$ 进制数代替后，再转 $\text{16}$ 进制。

如 $(567)_{8}$，先转为 $(000101110111)_{2}$，再转为 $(177)_{16}$。

小数同理。

• 计算机中带符号位的表示方法

原码：符号位为 $\text{0}$ 表示正数，符号位为 $\text{1}$ 表示负数，其余各位表示数值部分。

反码：

对于正数，它的反码表示与原码相同。

对于负数，则除符号位仍为 $\text{“1”}$ 外，其余各位 $\text{“1”}$ 换成 $\text{“0”}$，$\text{“0”}$ 换成 $\text{“1”}$。

对于 $\text{0}$，它的表示方法有两种，$\text{+0(00000)}$，$\text{-0(10000)}$。

补码：

正数的补码就是该正数本身。

对于负数：符号位不变，将其反码加 $\text{1}$。

• 信息存储单位

常见的有 $\text{bit(b)}$，$\text{Byte(B)}$，$\text{KiB}$，$\text{MiB}$，$\text{GiB}$。

$\text{1 B=8 b}$。

$\text{1 KiB=1024 B}$。

$\text{1 MiB=1024 KiB}$。

$\text{1 GiB=1024 MiB}$。

$\texttt{ASCII}$ 码：“美国信息交换标准代码” 的简称，最多可以表示 $\text{128}$ 个不同的符号，即一个字节。

$\text{‘0’ — 48}$，$\text{‘A’ — 65}$，$\text{‘a’ — 97}$。

• 视频文件大小的计算

例如：

现有一段 $\text{24}$ 分钟的视频文件，它的帧率是 $\text{30 Hz}$，分辨率是 $1920\times 1080$，每帧图像都是 $\text{32}$ 位真彩色图像，使用的视频编码算法达到了 $\text{25\%}$ 的压缩率。则这个视频文件占用的存储空间大小约是 （ ）。

$\text{A. 668 GiB}$

$\text{B. 334 GiB}$

$\text{C. 85 GiB}$

$\text{D. 500 GiB}$

$24\texttt{(24分钟)}\times 60\texttt{(每分钟60秒)}\times 30\texttt{(帧率)}\times 1920\times 1080\texttt{(分辨率)}\times 32\texttt{(32位)}\times 25\%\texttt{(25\%的压缩率)}\div 8\texttt{(1B=8b)}\div 1024\texttt{(1KiB=1024B)}\div 1024\texttt{(1MiB=1024KiB)}\div 1024\texttt{(1GiB=1024MiB)}$，约为 $\text{85 GiB}$，选 $\text{B}$。

• 逻辑运算

有 $\text{and(}\wedge\text{)}$，$\text{or(}\vee \text{)}$，$\text{not(}\neg \text{)}$，$\text{xor(}\oplus \text{)}$。

运算的优先级：$\text{not}$＞$\text{and}$＞$\text{or}$。

与运算：如果都为 $1$，则为 $1$，否则为 $0$。

或运算：如果都为 $0$，则为 $0$，否则为 $1$。

非运算：如果为 $1$，则为 $0$，否则为 $1$。

2.数据结构

• 线性表

概念：线性表是由 $n(n\ge 0)$ 个具有相同特性数据元素（结点） $a_{1}，a_{2}，\cdots，a_{n}$ 组成的有限序列。

长度：所含元素的个数，用 $n$ 表示，$n\ge ０$。

$\text{Ps}$：当 $\text{n=0}$ 时,表示线性表是一个空表，即表中不包含任何元素。

逻辑结构表示图：

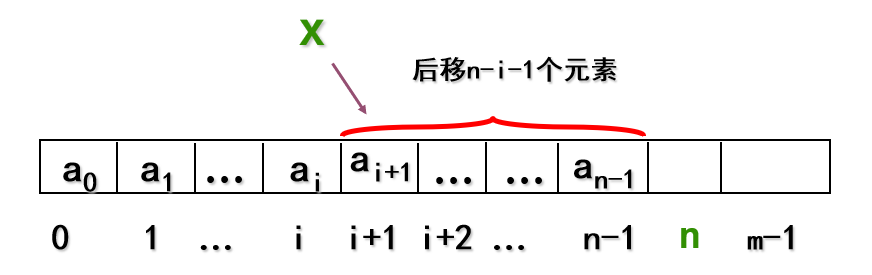
插入操作：

在表中下标为 $i$ 的元素 $a_{i}$ 后插入 $x$，后面元素往后移。若 $i=-1$，则将新元素 $x$ 插在最前面。

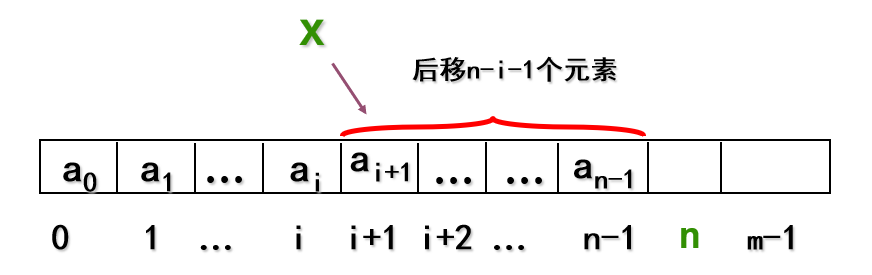
删除操作：

删除元素 $a_{i}$，后面元素往前移。

• 数组

概念：有序的元素序列。

二分查找：

框架：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

int binarySearch(int[] nums, int target) {
    int left = 0, right = ...;

    while(...) {
        int mid = (right + left) / 2;
        // 计算 mid 时需考虑溢出，因此最好写为 mid = left + (right - left) / 2
        if (nums[mid] == target) {
            ...
        } else if (nums[mid] < target) {
            left = ...
        } else if (nums[mid] > target) {
            right = ...
        }
    }
    return ...;
}

写法 $\text{1}$：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

// 左闭右闭式
int binarySearch(int[] nums, int target) {
    int left = 0; 
    int right = nums.length - 1; // 注意

    while(left <= right) { // 注意
        int mid = (right + left) / 2;
        if(nums[mid] == target)
            return mid; 
        else if (nums[mid] < target)
            left = mid + 1; // 注意
        else if (nums[mid] > target)
            right = mid - 1; // 注意
        }
    return -1;
}

写法 $\text{2}$：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

// 左闭右开式找左侧边界
int left_bound(int[] nums, int target) {
    if (nums.length == 0) return -1;
    int left = 0;
    int right = nums.length; // 注意

    while (left < right) { // 注意
        int mid = (left + right) / 2;
        if (nums[mid] == target) {
            right = mid;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid; // 注意
        }
    }
    return left;
}

写法 $\text{3}$：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

// 左闭右开式找右侧边界
int right_bound(int[] nums, int target) {
    if (nums.length == 0) return -1;
    int left = 0, right = nums.length;

    while (left < right) {
        int mid = (left + right) / 2;
        if (nums[mid] == target) {
            left = mid + 1; // 注意
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid;
        }
    }
    return left - 1; // 注意
}

最坏情况查找 $\left \lceil \log_{2}n \right \rceil$ 次。

排序

常考的有：选择排序、冒泡排序、插入排序、快速排序、希尔排序、堆排序、归并排序、基数排序。

• 树

树是典型的非线性结构，它是由 $n(n\ge 1)$ 个有限节点组成一个具有层次关系的集合。

常用的树为二叉树。

遍历：

先序遍历：根，左，右。

1
2
3
4
5
6
7

void preTrav(BiTree* root) {
  if (root) {
    cout << root->key << " ";
    preTrav(root->left);
    preTrav(root->right);
  }
}

中序遍历：左、根、右。

1
2
3
4
5
6
7

void midTrav(BiTree* root) {
  if (root) {
    midTrav(root->left);
    cout << root->key << " ";
    midTrav(root->right);
  }
}

后序遍历：左、右、根。

1
2
3
4
5
6
7

void lastTrav(BiTree* root) {
  if (root) {
    lastTrav(root->left);
    lastTrav(root->right);
    cout << root->key << " ";
  }
}

满二叉树/完美二叉树：所有叶结点的深度均相同的二叉树称为满二叉树/完美二叉树。

完全二叉树：只有最下面两层结点的度数可以小于 $2$，且最下面一层的结点都集中在该层的最左侧。

应用：堆排序，哈夫曼树。

算平均查找次数时可画搜索二叉树。

搜索二叉树是一种特殊有序的二叉树，如果一棵树不为空，并且如果它的根节点左子树不为空，那么它左子树上面的所有节点的值都小于它的根节点的值，如果它的右子树不为空，那么它右子树任意节点的值都大于他的根节点的值，它的左右子树也是二叉搜索树。

由此可见，如果对二叉搜索树进行中序排列（左中右），那么会得到一个从小到大的序列。

则将有序序列 $a$ 转为搜索二叉树后，每个结点对应深度即为这个结点所需的查找次数（根节点深度为 $1$ ）。

• 栈

遵循先进后出（$\texttt{DFS}$）。

• 队列

遵循先进先出（$\texttt{BFS}$）。

• 图

图是另一种非线性数据结构。在图结构中，数据结点一般称为顶点，而边是顶点的有序偶对。如果两个顶点之间存在一条边，那么就表示这两个顶点具有相邻关系。

入度：以顶点 $v$ 为终点的边的条数为该节点的入度。

出度：以顶点 $v$ 为起点的边的条数为该节点的出度。

分为有向图和无向图。

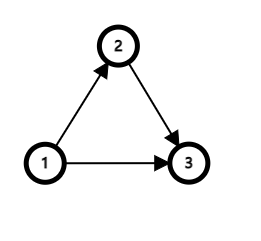
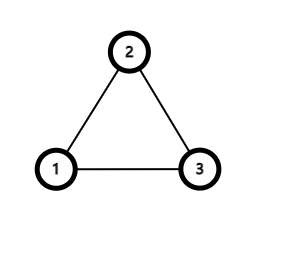
最短路算法有 $\color{red}\texttt{Floyd}$，$\color{red}\texttt{Dijkstra}$，$\texttt{Bellman-Ford}$，$\texttt{SPFA}$。

• 堆

算法：堆排序。

应用：$\text{STL}$ 大根堆——priority_queue <int,vector<int>,less<int> >q;。

$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$\text{STL}$ 小根堆——priority_queue <int,vector<int>,greater<int> > q;

• 链表

分为单向链表与双向链表。

$\large\texttt{单向链表}$：

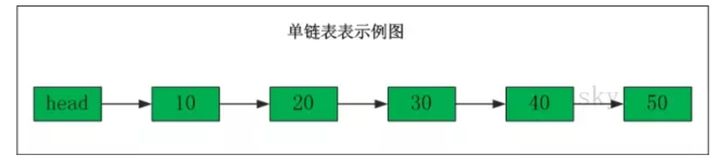
删除节点：

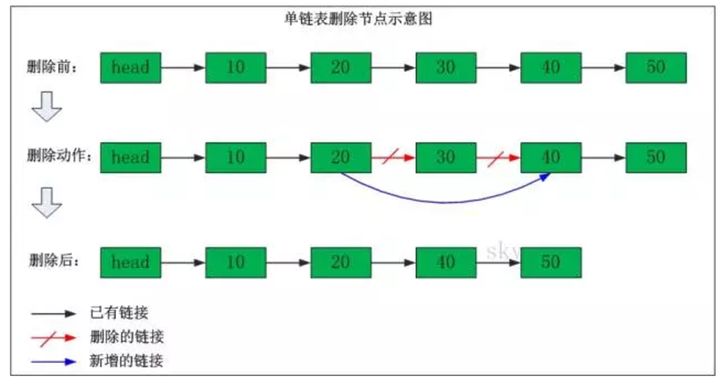
添加结点：

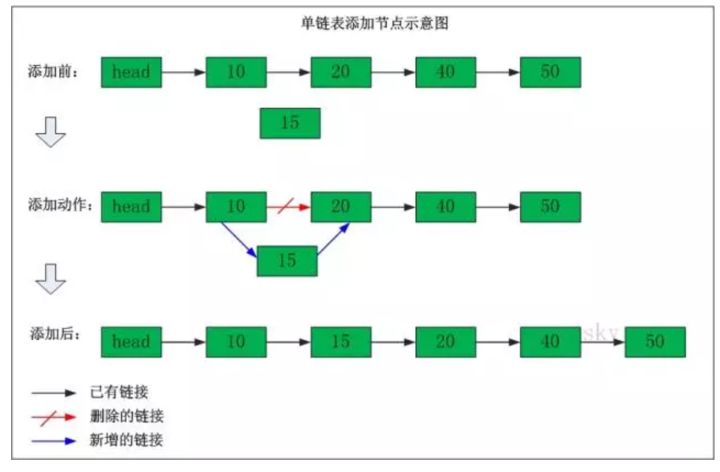
$\large\texttt{双向链表}$：

1
2
3
4
5
6
7

//双向链表节点结构
typedef struct dlink_node
{
    struct dlink_node *prev;
    struct dlink_node *next;
    void *val;  //能存储任意类型数据
}node;

删除结点：

1
2
3
4

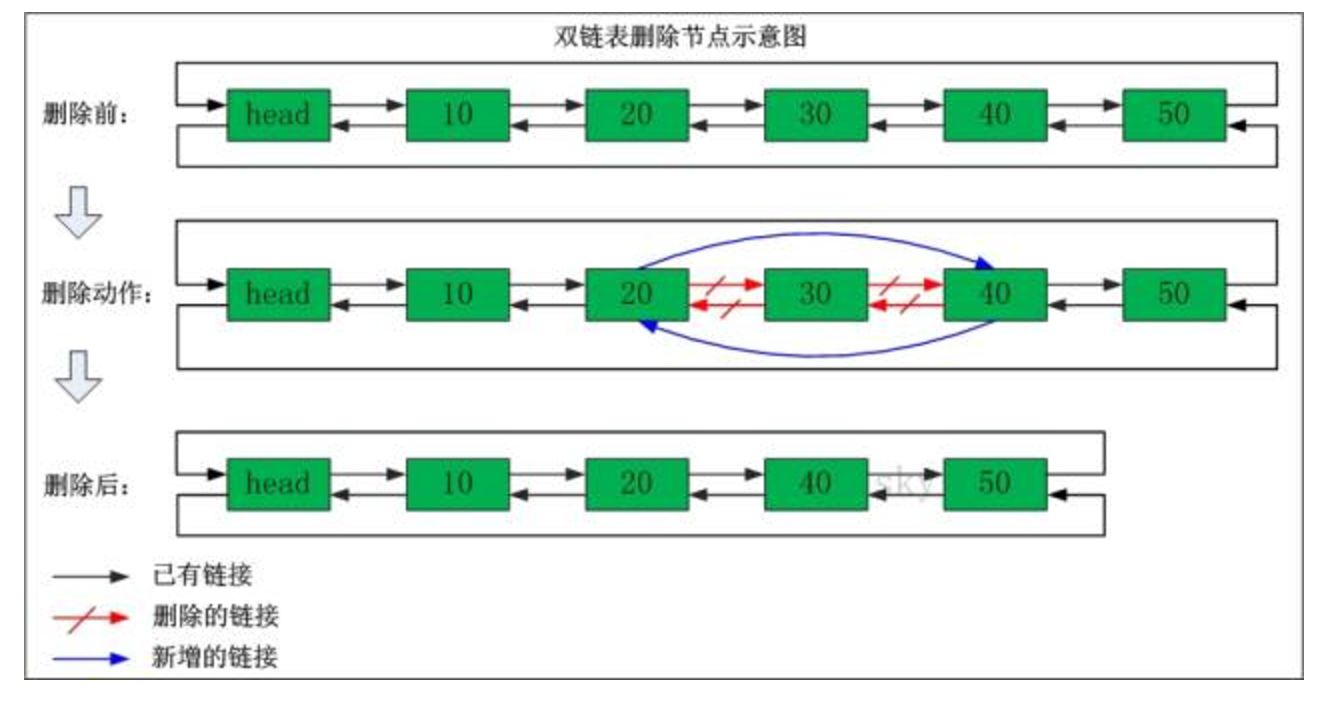
//删除节点pindex
pindex->next->prev = pindex->prev;
pindex->prev->next = pindex->next;
free(pindex); //注意释放节点

添加结点：

1
2
3
4
5

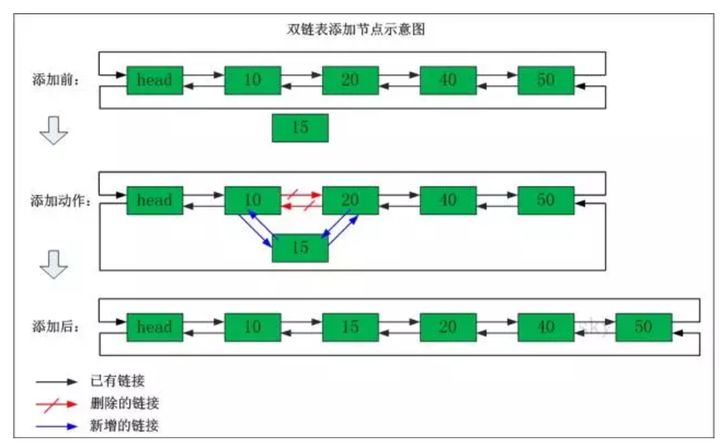
//将pnode节点插入到pindex之前
pnode->prev = pindex->prev;
pnode->next = pindex;
pindex->prev->next = pnode;
pindex->prev = pnode;

3.数学

• 时间复杂度

定义：在进行算法分析时，语句总的执行次数 $\text{T(n)}$ 是关于问题规模 $n$ 的函数，进而分析 $\text{T(n)}$ 随 $n$ 的变化情况并确定 $\text{T(n)}$ 的数量级。算法的时间复杂度，也就是算法的时间量度，记作：$\text{T(n)=O(f(n))}$。它表示随问题规模 $n$ 的增大，算法执行时间的增长率和 $\text{f(n)}$ 的增长率相同，称作算法的渐近时间复杂度，简称为时间复杂度。其中 $\text{f(n)}$ 是问题规模 $n$ 的某个函数。 这样用大写 $\text{O()}$ 来体现算法时间复杂度的记法，我们称之为大 $\text{O}$ 记法。一般情况下，随着 $n$ 的增大，$\text{T(n)}$增长最慢的算法为最优算法。

符号：

$\Theta $，可以理解为 $=$。

$\mathcal{O}$，可以理解为 $\le$。

$\Omega $，可以理解为 $\ge$。

$o$，可以理解为 $<$。

$\omega $，可以理解为 $>$。

主定理

$T(n)=aT\left(\frac{n}{b}\right)+f(n)$

1. 若函数 $n^{\log_{b} a}$ 更大，则 $T(n)=\Theta\left(n^{\log _{b} a}\right)$；
2. 若函数 $f(n)$ 更大，且满足 $a f(n/b) \leq c f(n)$，则 $T(n)=\Theta(f(n))$；
3. 若两函数相等，则 $T(n)=\Theta\left(n^{\log _{b} a} \log ^{k+1} n\right)$。

以上的大小比价, 都是渐进意义上的。

$\text{Ps}$：第三种情况，大多数时候 $k=0$。

https://zhuanlan.zhihu.com/p/113406812

• 排列组合

排列英文名叫 $\texttt{Arrangement}$ 或者 $\texttt{Permutation}$，下文统称为 P。

组合英文名叫 $\texttt{Combination}$，下文统称为 C。

$\mathcal{P}_{n}^{m}=\frac{n!}{(n-m)!}=n\times (n-1)\times \dots\times(n-m+1)$

$\mathcal{C}_{n}^{m}=\frac{n!}{(n-m)!m!}=\frac{n\times (n-1)\times \dots\times(n-m+1)}{m\times (m-1)\times \dots\times 1}$

组合数规律 $1$：

$\mathcal{C}_{n}^{m}=\mathcal{C}_{n}^{n-m}$

组合数规律 $2$：

$\mathcal{C}_{n}^{m-1}+\mathcal{C}_{n}^{m}=\mathcal{C}_{n+1}^{m}$

组合数规律 $3$：

$\mathcal{C}_{n}^{0}+\mathcal{C}_{n}^{1}+\dots+\mathcal{C}_{n}^{n}=2^{n}$

组合数规律 $4$：

$\mathcal{C}_{r}^{r}+\mathcal{C}_{r+1}^{r}+\dots+\mathcal{C}_{n}^{r}=\mathcal{C}_{n+1}^{r+1}$

组合数规律 $5$：

$\sum_{i=0}^{k} \mathcal{C}_{n}^{i} \mathcal{C}_{m}^{k-i}=\mathcal{C}_{m+n}^{k}$

经典模型：

当小球遇上盒子

默认为有 $n$ 个小球，$m$ 个盒子。

1. 球相同，盒子不同，不能有空盒

$ans=\mathcal{C}_{n-1}^{m-1}$

1. 球相同，盒子不同，可以有空盒

$ans=\mathcal{C}_{n+m-1}^{m-1}$

1. 球不同，盒子不同，可以有空盒

$ans=m^{n}$

其余均有些超纲，有兴趣的同学可以自行阅读链接文章。

拓展试题：P5824。

一般 $\begin{pmatrix}
n \\
m
\end{pmatrix}$ 表示组合数，$\begin{bmatrix}
n \\
m
\end{bmatrix}$ 表示第一类斯特林数，$\begin{Bmatrix}
n \\
m
\end{Bmatrix}$ 表示第二类斯特林数。

• 其余定理

推荐阅读：

https://www.cnblogs.com/Lrefrain/p/11353765.html

https://www.luogu.com.cn/blog/BotDand/lucas-xue-xi-bi-ji（推荐自己的，真不要脸）

4. 总结

终于咕完了，希望初赛 $\texttt{RP++}$ \kel。

5. 补充

• 各种数据类型占用的内存空间